Figure 2 shows the ways the block and tackle are used.
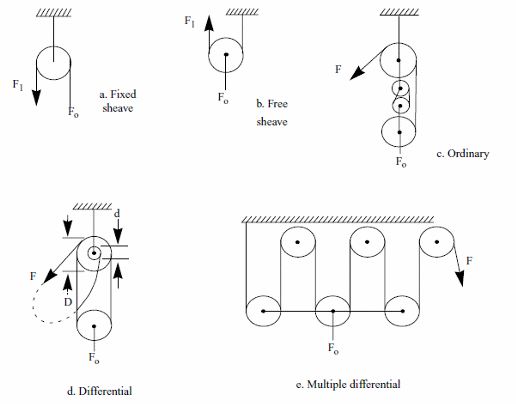
The mechanical advantage depends on the use:
Force (disregarding bearing friction and rope rigidity) :
Formula
a) Fixed Sheave or pulley
F1 = Fo
b) Free sheave or pulley
F1 = Fo/2
c) Ordinary pulley block
F1 - Fo/n
d) Differential pulley block
F1 = 1/2(1 - d/D)Fo
e) Multiple Differential Pulley Block
F1 = Fo/2n
Where:
F1 - Force required to raise ot lower the load
Fo - Load
n = number of pulleys
d, D - Diameter of the pulleys
Path of the Load
Formulas - (figure 3)
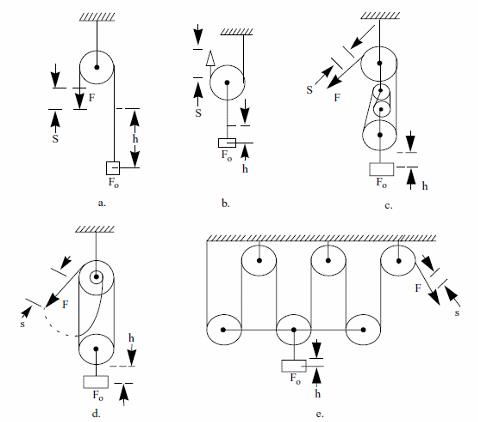
a) Fixed sheave
s = h
b) Free sheave
s = 2 x h
c) Ordinary pulley block
s = n x h
d) Differential pulley block
s = 2h/(1-d/D)
e) Multiple differential pulley block
h = D/2n
Moment of Force
Moment M of a force F about a point O is te perpendicular distance from point O to the line of action of force F times the force F.
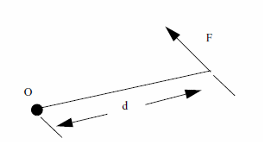
Formula
M = F x d
Where:
M is the moment
F is the force
d is the distance
Resultant forces: (figure 5)
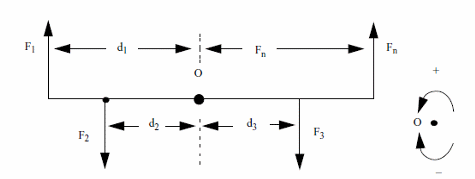
Formula
F1 x d1 + F2 x d2 + F3 x d3 + ..... Fn x dn = 0
Pbs: F may be positive or negative according the direction defined by clockwise or counterclockwise.



