Pulleys are used to change speed or torque when used with motors or other rotatory power sources.
The next formulas are used to calculate the theoretical mechanical advantage of pulley systems and the change of speed. See figure 1.
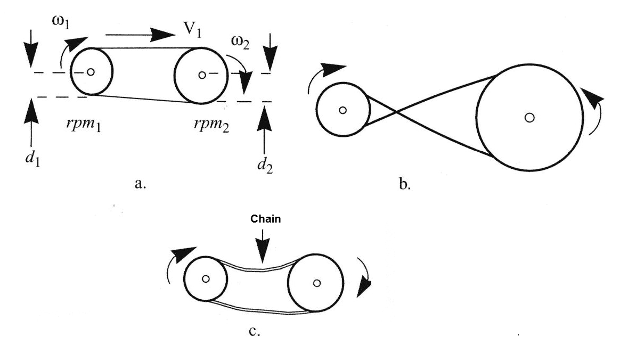
(a) Belt and pulley
(b) O-ring
(c) chain driver
Formulas
a) Change of speed:
tangential:
V1/V2 = d2/d1 (1)
angular:
ω1/ω2 = d2/d1 (2)
rpm
rpm1/rpm2 = d2/d1 (3)
Where: v1 and v2 are the tangential speed of the pulleys
ω1 and ω2 are the angular speed of the pulleys
rpm1 and rpm2 are the revolution per minute of the pulleys
d1 and d2 are the diameters of the pulleys
Obs: the speed of the belt is constant
b) Change of torque:
M1/M2 = d2/d1 (4)
Where: M1 and M2 are the torque
d1 and d2 are the diameters ot the pulleys
c) TMA:
TMA = M2/M1 = d1/d2 = ω1/ω2 = rpm2/rpm1 = v2 /v1 (5)
Where: TMA is the theoretical mechanical advantage
v1 and v2 are the tangential speed of the pulleys
ω1 and ω2 are the angular speed of the pulleys
rpm1 and rpm2 are the revolution per minute of the pulleys
d1 and d2 are the diameters of the pulleys
d ) Complex systems
Figure 2 shows a complex system using pulleys and belts. The next formulas are valid for calculus involving TMA, change of speed and torque.
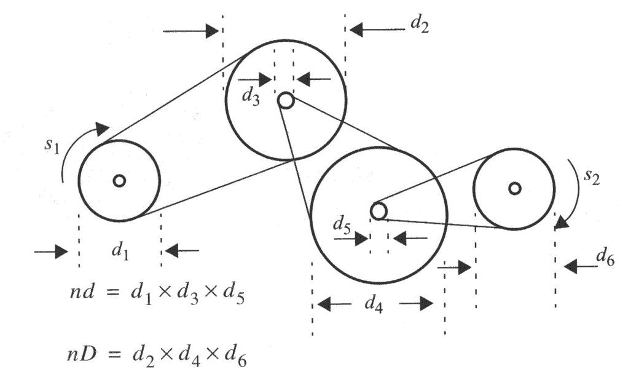
Formulas:
a) Change of speed
Tangential/Angular
S2 = S1 x nD/nd (6)
Where: S1 is the speed of the first pulley in train
S2 is the speed of the last pulley in train
nD is the product of the diameters on all drivers
nd is the product of diameters on all driven gears
b) Change of torque
M2/M1 = S1/S2 (7)
Where: M1 and M2 are the torque of the pulleys
S1 is the speed of the first pulley in train (angular or tangential)
S2 is the speed of the last pulley in train (angular or tangential)
c) TMA
TMA = M2/M1 = S2/S1 (8)



