Figure bellow shows the basic configuration where Rg is the generator internal resistance and RL the load resistance.
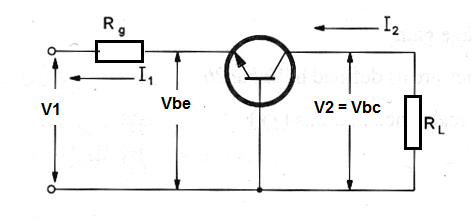
Note: the index "b" used with the hybrid parameters to indicate that they are common base parameters where suppressed in the next formulas to make easier their use. So instead write h21e we are using h21.
Formula 1
Current gain:
Gi = Ic / Ic
Gi = h21 / (1 + h22 x RL)
Where:
The quantities are as defined in table (MA096).
RL is the load resistance in ohm (Ω)
Formula 2
Voltage gain:
Gv = Vbc / Vbe
Gv = (h21 x RL) / (h11 + det h x RL)
Where:
GV is the voltage gain
Other quantities are defined in table (MA096).
RL is the load resistance in ohm (Ω)
Formula 3
Input resistance:
Rin = Ubc / Ic
Rin = (h11 + det x RL) / (1 + h22 x RL)
Where:
Rin is the input resistance in ohm (Ω)
Other quantities are defined as in table (MA096).
Formula 4
Output resistance:
Rout = Ubc / Ie
Rout = (h11 + RG) / (det h + h22 x RG)
Where
Rout is the output resistance in ohm (Ω)
RG is the generator resistance
The other quantities as defined in table (MA096)
Formula 5
Power gain:
Gp = Gi x Gu
Gp = (h212 x RL) / [ ( 1+ h21 x RL) x (h11 + det h x RL) ]
Where
Gp is the power gain
Gi is the current gain
Gu is the voltage gain
RL is the load resistance in ohm (Ω)
Other parameters as defined by table (MA096).
Derivated formulas:
Formula 6
When the input impedance is matched with the input resistance (Ri = RG) the following formula are used to calculate the power gain can be used:
Gp = (4 x RG x RL x H212) / [ RG(1 + h22 x RL) + (h11 + det h x RL) ]2
Where:
Gp is the power gain
Rg is the generator resistance in ohm (Ω)
RL is the load resistance in ohm (Ω)
Other parameters as defined by table (MA096).



