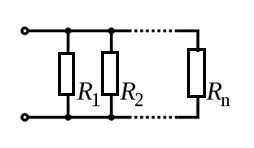
The equivalent conductance of a parallel association of resistor is equal to the sum of the conductances of the associated resistors. As conductance is defined as the inverse of resistance, we can write two formulas to calculate resistors wired in parallel.
Formula 1
G = G1 + G2 + ..... + Gn
Where:
G is the equivalent conductance of the association in siemens (S)
G1, G2, ... Gn are the condctances of the associated resistors in siemens (S)
Formula 2
Starting from G = 1/R (the conductance is the inverse of resistance), we can also write:
1/R = 1/R1 + 1/R2 + … 1/Rn
Where:
R is the equivalent resistance in ohm (Ω)
R1,R2... Rn are the associated resistances in ohm (Ω)
Formula 3
If n equal resistors are associated in parallel the equivalent resistance can be calculated by the next formula.:
R = R1 / n
Where:
R is the equivalent resistance in ohm (Ω)
R1 is the value of all associated resistors (all equal) in ohm (Ω)
n is the number of associated resistror
Important Properties:
a) All resistors are submted to the same voltage
b) The equivalent resistance is lower than the lowest associated resistance
c) The lowest resistance converts more power in heat
d) The highest current flows through the lowst resistance
Application Example:
Calculate the equivalent resistance of 20-ohm and 30-ohm resistor wired in parallel.
Data:
R1 = 30 Ω
R2 = 20 Ω
R = ?
Applying formula 1:
1/R = 1/30 + 1/20
Converting the terms in the second member of the equality to the same denominator:
1/R = 2/60 + 3/60
1/R = 5/60
Inverting both members in the equality:
R = 60/5 = 12 Ω



