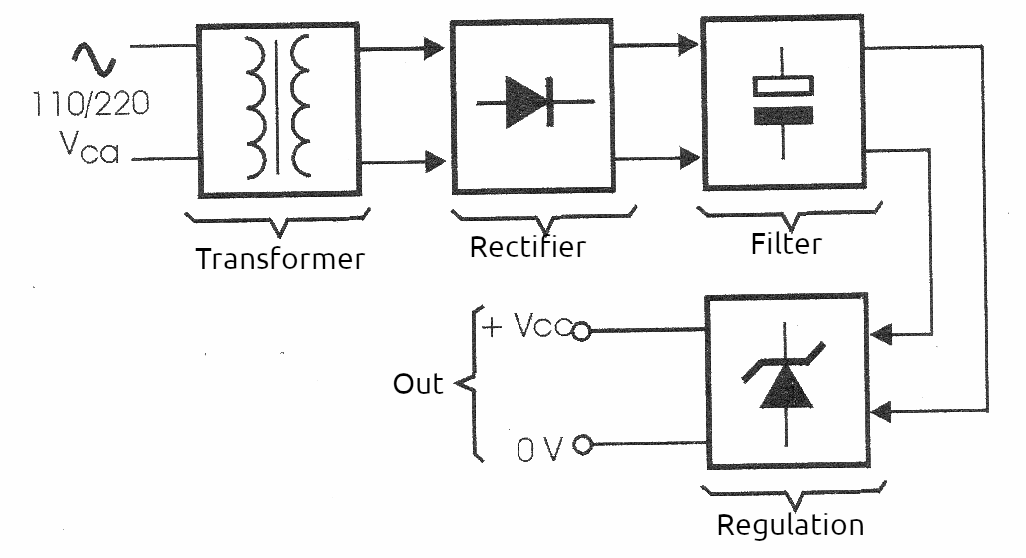
Common power supplies usually have a structure like the one shown in figure 1 where we have a transformer at the input that lowers the voltage of the power grid to a lower voltage that can be worked on by the rectification, filtering and regulation circuits.
However, in this type of power supply, the transformer is an inconvenient component, since it is not only heavy but also expensive and bulky. In many practical applications where space and cost are important, the possibility of eliminating this component should be analyzed. There are several solutions that allow the elimination of the transformer and that are used in practice. One of them is the one that uses switched or commutated power supplies, but their more complex structure is not always simple or convenient to implement. Another solution, which we discuss here, is to take advantage of the capacitive reactance of a capacitor to reduce the voltage.
Capacitive Reactance
When we connect a capacitor to an alternating current circuit, its charge and discharge represent an average current, which depends on both the value of this capacitor and the frequency, as shown in the formula below:
Xc: 1 / (2ΠfC)
Where:
Xc is the capacitive reactance in ohms
Π = constant = 3.14
F is the frequency in hertz
C is the capacitance of the capacitor in farads
As we can see, the capacitor behaves like a resistor when connected to an alternating current circuit and can function as a voltage reducer if connected in series with a load. The big advantage is that, while the resistor dissipates a power that is given by its resistance multiplied by the square of the current (P = R x I2), the capacitor does not dissipate power, hence its advantage. So, all we have to do in a transformer power supply design is to connect the capacitor in series with a rectification, filtering and regulation circuit, as shown in Figure 2.
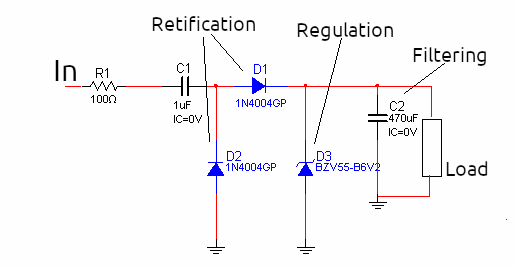
In this circuit, the capacitor determines the current in the load according to its value. Its reactance must be such that it causes the desired voltage drop with the current drained by the load, according to the frequency of the network and its voltage. We can think of it as a resistor whose resistance is Xc (capacitive reactance) connected in series with the load. From this, the basic problem will then be to calculate the components of this circuit, which we will teach now.
Calculating the Components.
The procedure that we give below is valid for simple sources up to about 50 mA of current. For the calculations, we then start with the capacitive divider shown in figure 3.
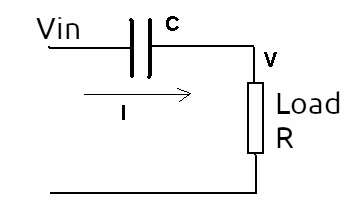
In this circuit, as the voltage across the load is much lower than the input voltage and therefore the voltage drop across the capacitor, we can ignore the load and directly consider a drop of 110 V or 220 V across the capacitor, as the case may be, with the desired current. In other words, we calculate what the value of the capacitor should be so that it has a capacitive reactance that results in the desired load current, in our case 20 mA or 0.02 A. We then start by calculating the value of C.
In this circuit we have:
Vin – 110 V
I = 0.02 A (20 mA)
F = 60 Hz
C = ?
With this data we then determine the impedance (Z) of the circuit for the 110 V network with a current of 0.02 A. This is given by the formula:
Z = Vin/I
Z = 110/0.02 = 5,500 ohms
This is the capacitive reactance that the capacitor must present in our circuit. We can calculate Xc, which is the capacitive reactance that the capacitor used in this circuit must have. The formula will be:
Xc: 1 / (2ΠfC)
For the calculated values we have:
5,500 = 1/(2 x 3.14 x 60 x C)
Therefore:
1/C = 2 x 3.14 x 60 x 5,500
C = 1/(2,072,400)
C = 0.000,000,482 Farads
C = 0.482 uF = 482 nF
Obviously, a polyester capacitor with at least 50% more than the peak value of the mains input voltage must be used.
As for the filtering capacitor, just use a sufficient value to have a reduced ripple. Although we can calculate this capacitor, a rule of thumb tells us that, for up to 12 V, we need 1,000 uF for each ampere. This means that a capacitor from 220 uF to 470 uF will be more than enough for our source.
Simple Power Supply Assembly without Transformer (3 to 12 V x 20 mA)
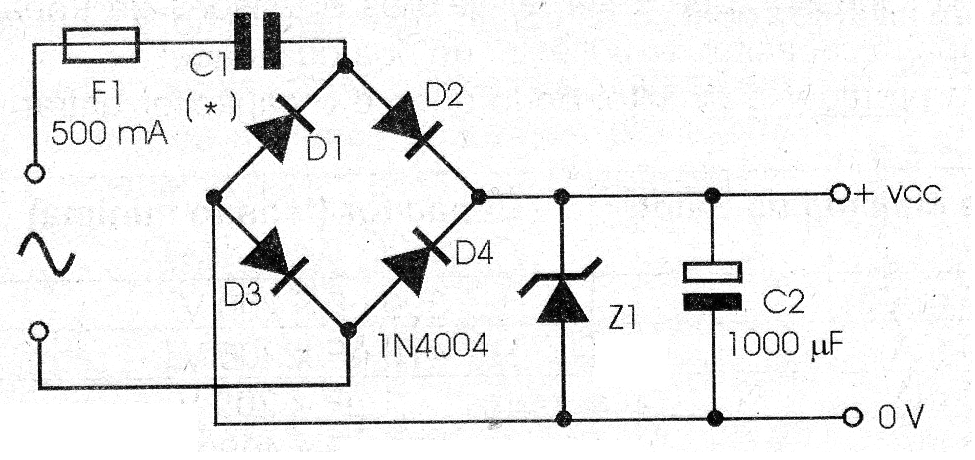
For applications where isolation from the power grid is not important, the transformer, which is an expensive, heavy and bulky component, can be dispensed with. Instead, the capacitive reactance of a good quality polyester capacitor is used to reduce the voltage of the power grid.
The project we present can operate on both 110 V and 220 V grids and provides a current of up to 20 mA. The output voltage depends solely on the zener diode used, ranging from 3 V to 12 V. Lower voltages can be obtained with a reference formed by common diodes, as shown in figure 4.
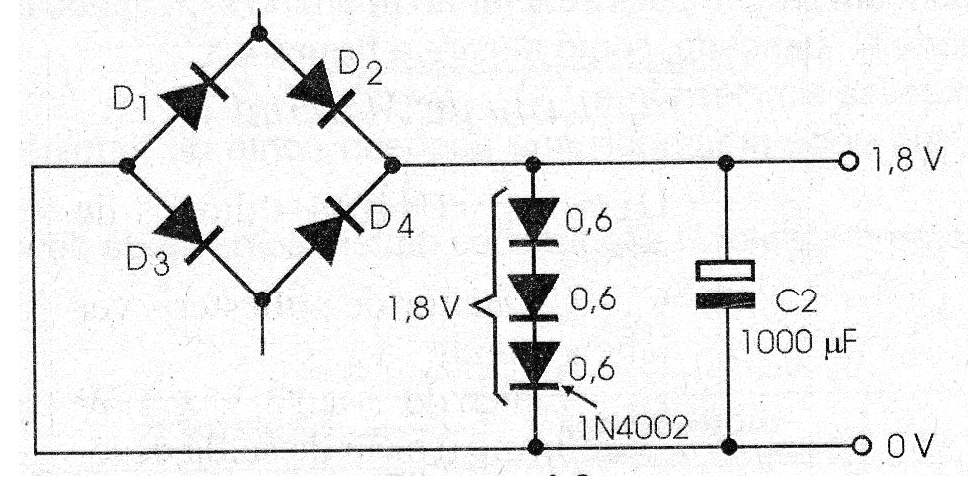
Each diode provides a voltage of around 0.6 V when used as a reference. Therefore, for 2.4 V, it is sufficient to use 4 diodes in series. An LED can also be used as a 1.6 V reference for red types. For yellow and green types, the reference will be 1.8 V and 2.1 V, as shown in Figure 5.
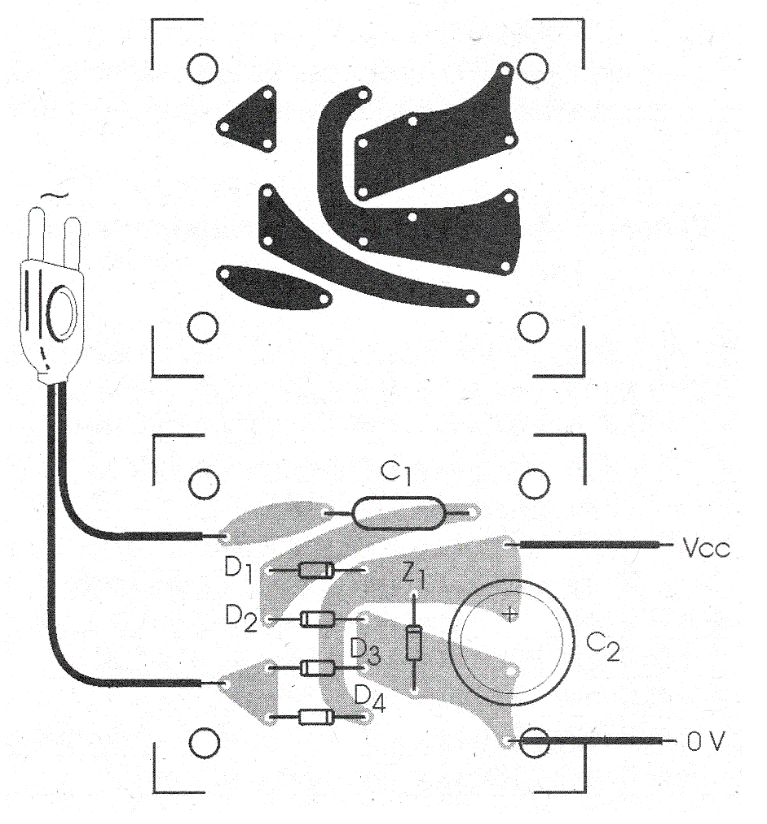
Its assembly requires no more than a small terminal bridge to support the components, as shown in Figure 7.
Of course, if the reader has the resources to design printed circuit boards, he/she can use the pattern in Figure 8 as a reference.

The critical component of this project is the capacitor, which must have values and working voltages
The input fuse is important to protect the circuit, since if the capacitor shorts out; the power supply must be turned off immediately. The electrolytic capacitor must have a working voltage slightly higher than that desired at the output. For example, for a 6 V output, use a 12 V or 16 V capacitor. The circuit fits in a small battery eliminator-type box that can be plugged into the network itself from any common outlet.
Material List
D1 to D4 – 1N4004 – silicon diodes
C1 – Polyester capacitor – see table and text
Z1 – 3 to 12 V x 1 W Zener – according to desired output voltage
C1 – 470 uF – electrolytic capacitor – see text
F1 – 500 mA – fuse
Miscellaneous:
Terminal bridge or printed circuit board, power cable, fuse holder, wires, solder, mounting box, etc.