This article is part gf my book Mechatronics Sourcebook now in a new edition originally written in portuguese and transleted into English. It explains how to making calculations using this mechanical arrangements.
Gears
There are two basic gear arrangements of gears shown by figure 1.
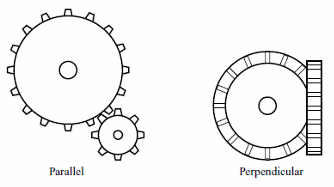
Obs: when two gears of unequal size are combined the smaller is usually called a pinion.
Figure 2 shows other types of gears.
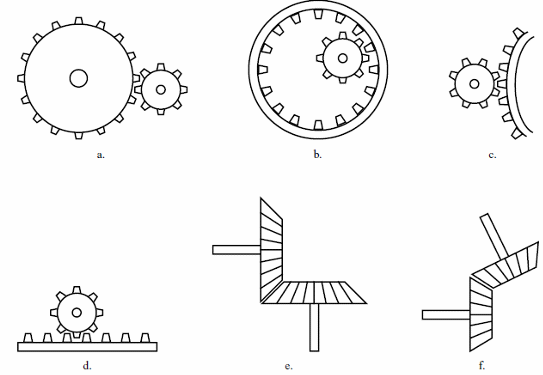
a) Helical spur
b) Rack and pinion
c) Sector gear
d) Linear gear
e) Miter gear
f) Bevel Gear
Formulas
a) Speed change
v1/v2 = n1/n2 (linear)
?2/?1 = n2/n1 (angular)
Where:
V1 and V2 are the tangential speed of the gears
n1 and n2 are the number of teeths
?1, ?2 are the tangential speed in rad/sec
b) Mechanical Advantage:
TMA = V2/V1
TMA = n2/n1
or
TMA = ?2/?1
Where
TMA is the theoretical mechanical advantage:
V1 and V2 are the tangential speed of the gears
n1 and n2 are the number of teeths
?1, ?2 are the tangential speed in rad/sec
c) Torque Change
TMA = n1/n2
Where:
n1 is the number of teeth on the driven gear
n2 is the number of teeth on the driven gear
M2/M1 = n2/n1
M2/M1 = V1/V2
M2/M1 = ?1/?2
Where:
M1 and M2 are the turning moment
V1 and V2 are the tangential speed of the gears
n1 and n2 are the number of teeths
?1, ?2 are the tangential speed
Obs: friction is disconsidered
d) Teeths versus diameter
n1/n2 = d/D
Where:
n1 and n2 are the number of teeths
d and D are the diameter of the gears
Figure 3 shows all the situations involved in the previous formulas.

Table -Speed Units Equivalence Table
| Units | m/s | m/min | km/h | ft/s | ft/min | mile/h | knot |
| m/s | 1 | 60 | 3.60 | 3.281 | 196.85 | 2.237 | 1.943 |
| m/min | 0.01667 | 1 | 0.050 | 0.05468 | 3.281 | 0.03728 | 0.03238 |
| km/h | 0.02778 | 16.67 | 1 | 0.9113 | 54.68 | 0.6214 | 0.5396 |
| ft/s | 0.3048 | 18.288 | 1,097 | 1 | 60 | 0.6818 | 0.5921 |
| ft/min | 0.0051 | 0.3048 | 0.01687 | 0.0183 | 1 | 0.01136 | 0.00987 |
| mile/h | 0.4470 | 26.42 | 1.609 | 1.467 | 88 | 1 | 0.8684 |
| knot | 0.5148 | 30.887 | 1.8532 | 1.6889 | 101.333 | 1.1515 | 1 |
Gear Boxes
Gear boxes are used to change speed or torque in mechatronic projects. The number, the size and the number of teeths determine the TMA of a gearbox or the number of times the torque or the speed is multiplied.
Figure 4 shows some gearboxes used to change the speed and increase the mechanical advantage.
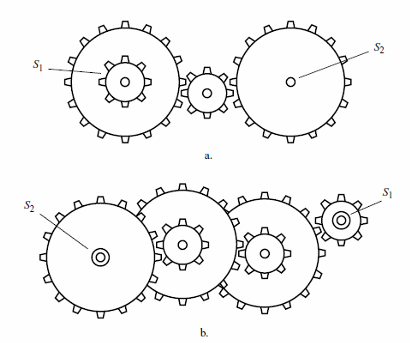
Formulas
a) Changing the speed:
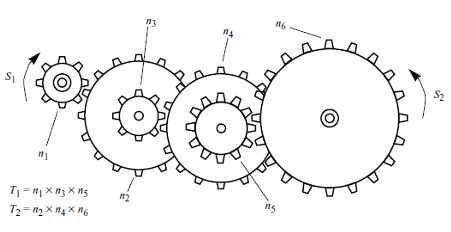
S2 = S1 x T1/T2
Where:
S1 is the speed of the first shaft in train
S2 is the speed of the last shaft in train
T1 is the product of the teeth on all drivers
T2 is the product of teeth oin all driven gears
Speed can be calculated in revolution per second, cm/s (tangential) or degrees per second (angular)
b) Changing the Torque:

TMA = T1/T2
Where:
T1 is the product of the teeth on all drivers
T2 is the product of teeth oin all driven gears
TMA is the theoretical mechanical advantage
Obs: friction is disconsidered
The Bevel Gear
Bevel gears are used if the shafts are not parallel as shown by figure 7 They are used to change the direction of a motion.
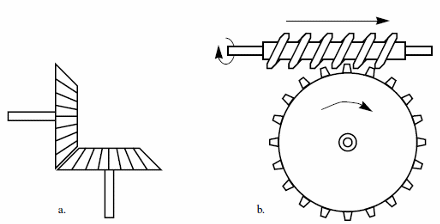
Figure shows two main types of bevel gars: (a) the mitter gear and the spiral gear.
For the spiral bevel gear the next formula is valid:
Formula
v = n1 x 2 x ? x R
Where:
V is the tangential speed of the circular gear
n1 is the number of steps advanced by the worm in one turn or revolution
? is the constant 3,14
R is the radius of the circular gear (diameter/2)
ITIONAL GEAR DESIGNERATURE AND SOFTWARE
Pulleys
Pulleys are used to change speed or torque when used with motors or other rotatory power sources.
The next formulas are used to calculate the theoretical mechanical advantage of pulley systems and the change of speed. See figure 8.
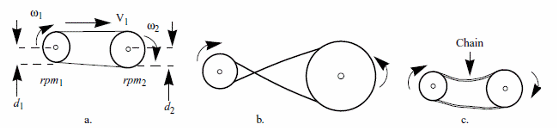
(a) Belt and pulley
(b) O-ring
(c) chain driver
Formulas
a) Change of speed:
tangential:
V1/v2 = d2/d1
angular:
?1/?2 = d2/d1
rpm
rpm1/rpm2 = d2/d1
Where:
v1 and v2 are the tangential speed of the pulleys
?1 and ?2 are the angular speed of the pulleys
rpm1 and rpm2 are the revolution per minute of the pulleys
d1 and d2 are the diameters of the pulleys
Obs: the speed of the belt is constant
b) Change of torque:
M1/M2 = d2/d1
Where:
M1 and M2 are the torque
d1 and d2 are the diameters ot the pulleys
c) TMA:
TMA = M2/M1 = d1/d2 = ?1/?2 = rpm2/rpm1 = v2 /v1
Where:
TMA is the theoretical mechanical advantage
v1 and v2 are the tangential speed of the pulleys
?1 and ?2 are the angular speed of the pulleys
rpm1 and rpm2 are the revolution per minute of the pulleys
d1 and d2 are the diameters of the pulleys
d ) Complex systems
Figure 9 shows a complex system using pulleys and belts. The next formulas are valid for calculus involving TMA, change of speed and torque.
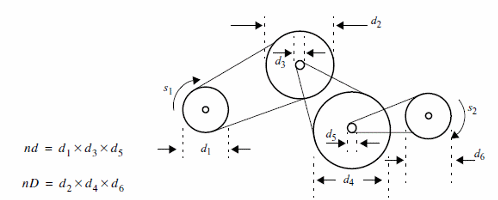
Formulas:
a) Change of speed
Tangential/Angular
S2 = S1 x nD/nd
Where:
S1 is the speed of the first pulley in train
S2 is the speed of the last pulley in train
nD is the product of the diameters on all drivers
nd is the product of diameters on all driven gears
b) Change of torque
M2/M1 = S1/S2
Where:
M1 and M2 are the torque of the pulleys
S1 is the speed of the first pulley in train (angular or tangential)
S2 is the speed of the last pulley in train (angular or tangential)
c) TMA
TMA = M2/M1 = S2/S1



