The equivalent resistance of resistors wired in series is equal to the sum of the resistances of each associated resistor.
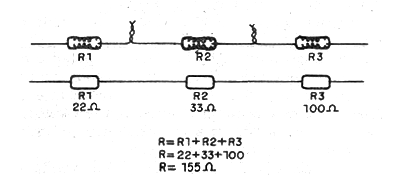
Formula 1
R = R1 + R2 + R3 + .... + Rn
Where:
R is the equivalent resistance in ohm (Ω)
R1, R2, R3... Rn are the associated resistances in ohm (Ω)
Derivated Formulas
Formula 2
Particular case:
All the associated resistances are equal (R1 = R2 = R3 = …. = Rn)
R = n x R1
Where:
R is the resistance in ohm (Ω)
n is the numero of associated resistances
R1 is the value of the associated resistances in ohm (Ω)
Important Properties:
a) The greater resistance converts the greatest amount of Power in heat.
b) The amount of current flowing by all resistor is the same.
c) The equivalent resistance is greater than the greatest associated resistance.
d) The greatest resistance is submitted to the greatest voltage.
Application Example:
What is the equivalent resistance of na association where resistors of 20, 50 and 120 Ω are wired in series? Which resistor dissipates more heat?
Data:
R1 = 20 Ω
R2 = 50 Ω
R3 = 120 Ω
R = ?
Using formula1:
R = 20 + 50 + 120 = 190 Ω
R3 (120 Ω) converts more Power in heat. Use Ohm´s Law and Joule´s Law to calculate the amount of Power converted in heat when the association is submitted to a certain voltage.



